堆疊 Stack

本文同步發布於 2023 iThome 鐵人賽：那些前端不用會，但是可以會的資料結構與演算法系列文中。

我們可以把 Stack 看成是一個弱化的陣列，它只有兩個改變長度的方法：push 和 pop。用生活中的例子來描述 Stack，可以想像有一個用來裝書本的箱子，每次只能在最上面放入或取出一本書，這就是 Stack 的 push 和 pop。而且最先放入的書本會在最底下，必須要先取出最上面的書本才能取出下面的書本，這就是 Stack 的“後進先出”（Last In First Out，LIFO）特性。

圖片來源：pexels.com

還有一個就是我們常用的網站 Stack Overflow，它的名字就是來自於 Stack 這個資料結構，前面說到有個箱子用來裝書本，那麼如果我們不斷放書進去，當箱子已經被裝滿時，我們還繼續放書進去，那麼箱子就會溢出，書本就會掉出來，這就是 overflow，現在我們再回頭看看這個網站的 Logo，是不是突然知道為什麼它會這樣設計了呢？

Stack 的特點與概念

Stack 有如下的特點：

Stack 中的元素必須遵循 LIFO 的原則。
只能從最頂端進行加入和移除的操作。

Stack 的相關概念如下：

頂端和底端：允許插入和刪除的一端稱為頂端（Top），另一端稱為底端（Bottom）。
push：將元素加入 Stack 的操作。
pop：將元素從 Stack 中取出的操作。

push 和 pop 的操作示意圖如下：

Stack 的 push 和 pop 操作示意圖

Stack 的相關方法

接著來看 Stack 的相關方法：

push：推入元素
pop：彈出元素
isEmpty：判斷 Stack 是否為空
size：回傳 Stack 的長度
top 或 peek：回傳 Stack 最頂端的元素

C++ 中取得 Stack 最頂端元素的方法叫 top，而 Java 中則是 peek。

Stack 的實作方式很簡單，就是把陣列再包裝一層，讓陣列只能從最後面插入和刪除元素，這樣就可以達到 Stack 的效果。

在開始之前，我們先來將單元測試給打開，這樣我們可以透過測試即時看到我們的程式碼是否正確。首先，我們打開系列文專案的 day04-stack/Stack.spec.js 檔案，然後將測試程式碼上的 describe.skip 的 skip 去掉：

describe.skip('Stack', () => {
describe('Stack', () => {
  // ...
})

然後執行我們的測試指令 pnpm test:ui，就可以在瀏覽器中看到測試結果了：

一開始都會是失敗的，因為我們還沒開始實作 Stack，接下來就讓我們開始實作 Stack 吧！

實作程式碼如下：

class Stack {
  // 使用 # 讓它是私有屬性，讓外部無法直接存取，
  // 這樣就可以限定只能透過 push 和 pop 來對其進行操作
  #items = [];

  push(data) {
    this.#items.push(data);
  }

  pop() {
    return this.#items.pop();
  }

  size() {
    return this.#items.length;
  }

  isEmpty() {
    return this.#items.length === 0;
  }

  peek() {
    return this.#items[this.#items.length - 1];
  }

  top() {
    return this.peek();
  }

  toString() {
    return this.#items.toString();
  }

  clear() {
    this.#items.length = 0;
  }
}

將上面的程式碼實作到 day04-stack/Stack.js 裡的 Stack 類別後，我們可以檢查一下我們的測試是否通過了：

確認測試通過後，讓我們用剛才實作的這個 Stack 來套用到下面的應用場景中。

Stack 的應用

1. 逆序輸出

Stack 最大的特點就是後進先出，所以逆序輸出是一個經常使用到的場景。先將所有元素依序 push 進到 stack 中，再依序 pop 出來就可以達到逆序的效果。

例如大家最常用的 ctrl + z、瀏覽器的上一頁。

2. 語法檢查，例如括號是否成對

這個應用場景是在編譯器中，編譯器會檢查程式碼中的括號是否成對，如果沒有成對就會報錯。例如：{[()]}這個括號就是成對的，而{[(]}這個括號就是沒有成對的，編譯器會報錯。它其實也是 LeetCode 上的一道題目，20. Valid Parentheses。

這道題是 Stack 的經典題，但是一般初學者可能沒辦法直接聯想到 Stack，大部分人（像是我一開始）都會去試著數左括號跟右括號的數量有沒有對上，然後就會發現如果是這樣 ([)] 的字串會無法正確判斷，因為不只括號數要對，它的出現順序也必須要合理，那麼我們怎麼把它跟剛才學的 Stack 做連結呢？

用圖解來看就是像這樣：

我們一開始先準備一個 Stack，然後依序遍歷每個括號：

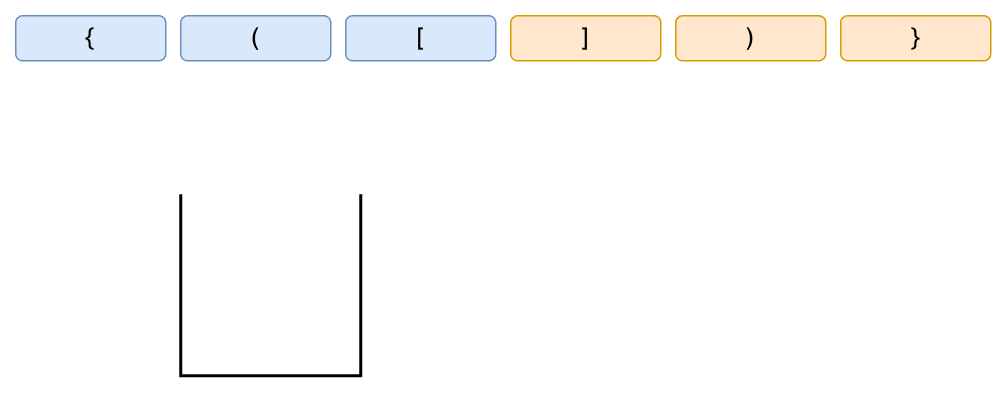
只要遇到左括號（開啟符號）就將它推入 Stack 中記錄各個括號的開啟順序：

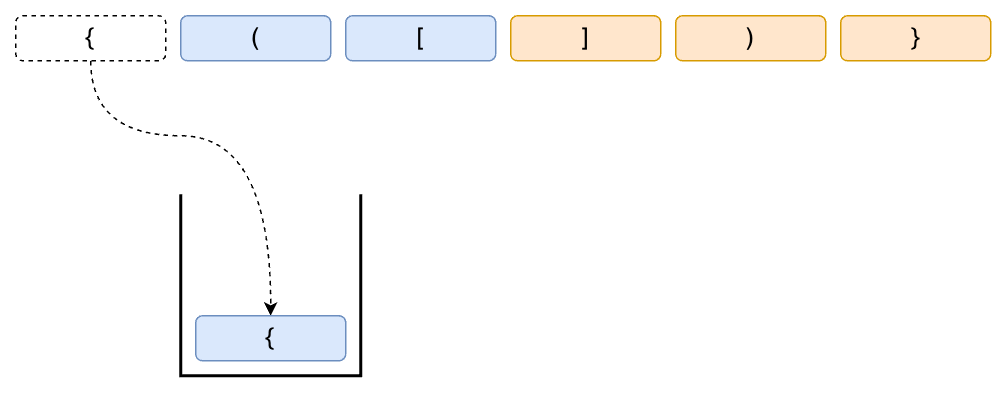
遇到右括號（關閉符號）我們就從 Stack 中彈出最後一次開啟的左括號，然後比較這兩個括號是否能成對：

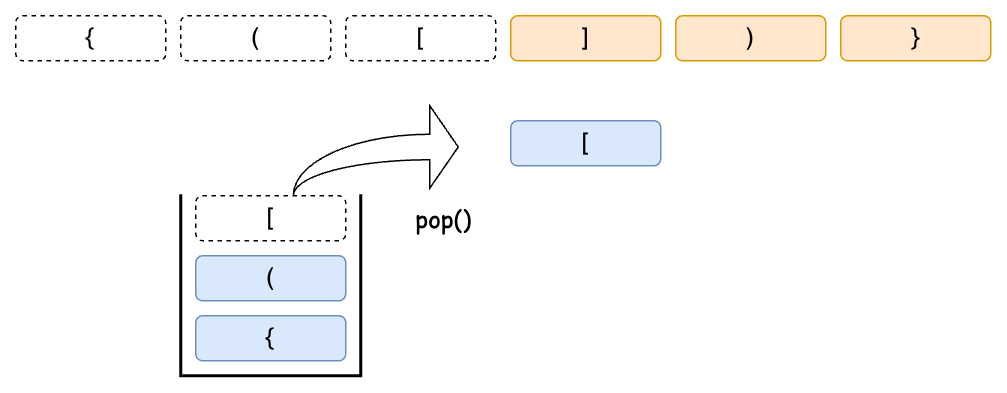
如果發現無法配對，代表我們這組括號對不合法，因為它必須依照後開啟先閉合的規則；如果配對成功我們就繼續往下遍歷，最後還要檢查我們的 Stack 是否已經清空，因為它有可能只有開啟就沒有關上了。

具體的實作如下：

function match(s) {
  const stack = new Stack();
  for (let i = 0; i < s.length; i++) {
    const c = s.charAt(i);
    switch (c) {
      case ')':
        if (stack.pop() === '(') {
          break;
        }
        return false;
      case ']':
        if (stack.pop() === '[') {
          break;
        }
        return false;
      case '}':
        if (stack.pop() === '{') {
          break;
        }
        return false;
      case '(':
      case '[':
      case '{':
        stack.push(c);
        break;
    }
  }
  return stack.isEmpty();
}

// 實際 console 看看結果或是直接 run 單元測試
console.log(match('{[()]}')); // true
console.log(match('{[(])}')); // false

3. 進位轉換

十進位 N 和其他 d 進位的轉換，解決的方式有很多種，其中一個簡單的算法基於下列原理：

$N = (N \div d) * d + N \mod d$ （其中：mod 是取餘數）

例如 (2007)10 = (3727)8，其運算過程如下：

十進位轉成八進位運算過程

可以看到上述過程是從低位到高位產生八進位的各個數位，然後從高位到低位輸出，結果數位的使用有後出現先使用的特性，所以可以使用 Stack 來解決這個問題。

// 十進位轉成二進位
function decimalToBinary(decimalNumber) {
  const stack = new Stack();
  let number = decimalNumber;
  let binaryString = '';

  while (number > 0) {
    stack.push(number % 2);
    number = Math.floor(number / 2);
  }

  while (!stack.isEmpty()) {
    binaryString += stack.pop();
  }

  return binaryString || '0';
}

decimalToBinary(5); // 101
decimalToBinary(10); // 1010

// 通用進位轉換
function convertDecimalToBase(dec, base) {
  const stack = new Stack();
  let number = dec;
  let ret = '';
  const digits = '0123456789ABCDEF';

  while (number > 0) {
    stack.push(number % base);
    number = Math.floor(number / base);
  }

  while (!stack.isEmpty()) {
    ret += digits[stack.pop()];
  }

  return ret || '0';
}

convertDecimalToBase(10, 2) // 1010
convertDecimalToBase(10, 8) // 12
convertDecimalToBase(10, 16) // A

4. 表達式求值

表達式求值是 stack 應用的一個典型例子。這裡介紹一種簡單直觀、廣為使用的算法，通常稱為「算符優先法」。

要把一個表達式翻譯成正確求值的一個機器指令序列，或者直接對表達式求值，首先要能夠正確解釋表達式。例如要對下述表達式求值：

$4 + ((6 - 10) + 2 \times 2) \times 2$

首先要理解四則運算的規則

先乘除後加減
從左算到右
括號優先算

因此這個算術表達式的計算順序應為：

$4 + ((6 - 10) + 2 \times 2) \times 2 = 4 + (- 4 + 4) \times 2 = 4 + 0 \times 2 = 4$

任何一個表達式都是由操作數（operand）和運算子（operator）和分隔符（delimiter）組成。分隔符就是小括號，運算子包括加減乘除，以及更複雜的求餘、三角函數等。這裡我們只討論簡單的算術表達式，所以運算子只有加減乘除。

我們把運算子和分隔符都統稱為算符，根據上面三條規則，在運算每一步時，任意兩個相繼出現的算符 θ1 和 θ2 之間的優先關係最多是下面三種關係：

θ1 < θ2，即 θ1 的優先級比 θ2 低
θ1 = θ2，即 θ1 的優先級和 θ2 相同
θ1 > θ2，即 θ1 的優先級比 θ2 高

這種優先關係如下表所示：

θ1\θ2	+	-	*	/	(	)
+	>	>	<	<	<	>
-	>	>	<	<	<	>
*	>	>	>	>	<	>
/	>	>	>	>	<	>
(	<	<	<	<	<	=
)	>	>	>	>		>

由規則 3 可知，+、-、* 和 / 為 θ1 時優先度均低於“(”，但高於右括號“)”。基於此，首先我們要來討論如何使用算符優先演算法來實作表達式求值。

為了實作這個演算法，我們需要使用兩個 stack，一個用來儲存操作數或運算結果，另一個用來儲存算符。

這個演算法的基本思想如下：

建立兩個 stack：操作數（OPND）stack 和運算符（OPTR）stack。
依次讀入表達式中的每個元素，若是操作數則存入 OPND stack，若是運算符則與 OPTR stack 的頂端運算符比較優先級再作相應處理。
若該運算符優先級高於 OPTR stack 的頂端運算符，則該運算符直接進入 OPTR stack；反之，則從 OPTR stack 中彈出一個運算符，並從 OPND stack 中彈出兩個數進行運算，運算結果存入 OPND stack。
重複步驟 2，直到將該運算符加入 OPTR stack。
表達式讀取結束，若兩個 stack 都不為空，則依次彈出 OPTR stack 中的運算符和 OPND stack 中的兩個操作數進行運算，再將結果存入 OPND stack，直到 OPTR stack 為空，OPND stack 中只剩一個數，即為最後的運算結果。
中間若出現差錯，例如最後 OPND stack 中不只一個數，則表示表達式出錯。

下面是完整實作程式碼：

function evaluate(expression) {
  const OPND_stack = new Stack();
  const OPTR_stack = new Stack();
  // 遍歷這個表達式
  for (let i = 0; i < expression.length; i++) {
    let c = expression.charAt(i);
    // 如果是數字，也就是操作數
    if (isDigit(c) || c == '.') {
      let stringBuilder = '';
      // 操作數的拼接，包含小數點
      while (i < expression.length && (isDigit((c = expression.charAt(i))) || c == '.')) {
        stringBuilder += c;
        i++;
      }
      // 操作數 push 到 OPND_stack
      OPND_stack.push(Number(stringBuilder));
      // 跳過本次迴圈，i 的值已經增加過，所以要減回來
      i--;
      continue;
    } else {
      // 如果是運算符
      outer: while (!OPTR_stack.isEmpty()) {
        switch (precede(OPTR_stack.top(), c)) {
          case '<':
            // 如果 OPTR_stack 的 top 運算符小於 c，那麼 c 直接入 OPTR_stack
            OPTR_stack.push(c);
            break outer;
          case '=':
            // 如果 OPTR_stack 的 top 運算符等於 c，那麼只有一種情況，左右括號相遇，直接 pop 出 "("
            OPTR_stack.pop();
            break outer;
          case '>':
            // 如果 OPTR_stack 的 top 運算符大於 c
            const operator = OPTR_stack.pop();
            // 如果有多餘的運算符卻沒有操作數可以計算，那麼這個表達式是錯誤的
            try {
              const opnd2 = OPND_stack.pop();
              const opnd1 = OPND_stack.pop();
              const result = operate(opnd1, operator, opnd2);
              OPND_stack.push(result);
            } catch {
              console.log('表達式錯誤!');
              return;
            }
            break;
        }
      }
      // 如果 OPTR_stack 是空的，那麼直接 push c
      if (OPTR_stack.isEmpty()) {
        OPTR_stack.push(c);
      }
    }
  }
  while (!OPTR_stack.isEmpty()) {
    const operator = OPTR_stack.pop();
    // 如果有多餘的運算符卻沒有操作數可以計算，那麼這個表達式是錯誤的
    try {
      const opnd2 = OPND_stack.pop();
      const opnd1 = OPND_stack.pop();
      const result = operate(opnd1, operator, opnd2);
      OPND_stack.push(result);
    } catch {
      console.log('表達式錯誤!');
      return;
    }
  }
  if (OPND_stack.size() === 1) {
    return OPND_stack.pop();
  } else {
    console.log('表達式錯誤!');
    return;
  }
}

const isDigit = (c) => /[0-9]/.test(c);
// 比較兩個運算符的優先級大小
const precede = (θ1, θ2) => {
  if (θ1 == '+' || θ1 == '-') {
    if (θ2 == '+' || θ2 == '-' || θ2 == ')') {
      return '>';
    } else {
      return '<';
    }
  } else if (θ1 == '*' || θ1 == '/') {
    if (θ2 == '(') {
      return '<';
    } else {
      return '>';
    }
  } else if (θ1 == '(') {
    if (θ2 == ')') {
      return '=';
    } else {
      return '<';
    }
  } else if (θ1 == ')') {
    return '>';
  }
  return '>';
};
// 執行運算
const operate = (opnd1, optr, opnd2) => {
  switch (optr) {
    case '+':
      return opnd1 + opnd2;
    case '-':
      return opnd1 - opnd2;
    case '*':
      return opnd1 * opnd2;
    case '/':
      return opnd1 / opnd2;
  }
  return 0;
};

我們最後再來檢查一下所有測試是不是都通過了：

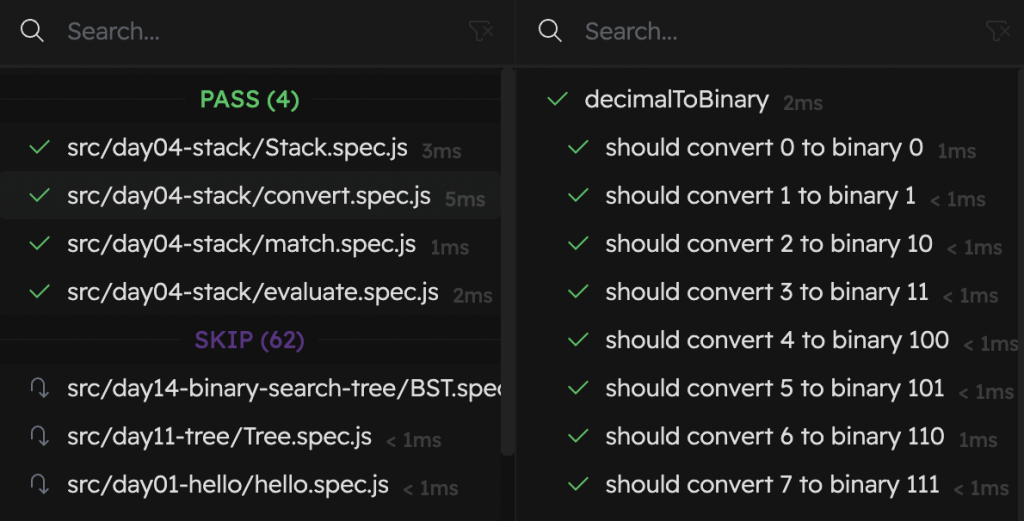
今天我們介紹了 stack 結構也說明了系列文專案的使用方式，在之後大部分的程式碼實作的檢查我都會交給單元測試來做，大家可以在實作前先觀察測資了解一下需求，然後就可以專注在程式碼上，也能順便體驗到由紅燈轉綠燈的樂趣。

參考資料

《JavaScript 算法：基本原理與代碼實現》

堆疊 Stack ​

Stack 的特點與概念 ​

Stack 的相關方法 ​

Stack 的應用 ​

1. 逆序輸出 ​

2. 語法檢查，例如括號是否成對 ​

3. 進位轉換 ​

4. 表達式求值 ​

參考資料 ​