合併排序法 Merge Sort

本文同步發布於 2023 iThome 鐵人賽：那些前端不用會，但是可以會的資料結構與演算法 系列文中。

shell sort 給我們帶來一個新思路，將一個問題拆分成幾個小規模的子問題，然後用現成的方案解決這些子問題，再慢慢合併來解決原問題。後來的人們稱這種思路為分治法（Divide and Conquer）。

當解決一個給定問題，演算法需要一次或多次遞迴呼叫自身來解決相關的子問題時，這種演算法通常是採用了 D&C 的策略。分治模式在每 1 層遞迴時都有 3 個步驟：

1. 分解：將原問題分解成一系列子問題。
2. 解決：遞迴地求解各子問題，若子問題足夠小則直接求解。
3. 合併：將子問題的解合併成原問題的解。

merge sort 的分解部分被分解得非常徹底，一口氣將每個子陣列切到只剩 1 個元素，因為長度為 1 的陣列可以看作是已排序的。然後將相鄰的兩個有序陣列合併成一個有序陣列，並不斷遞迴這個過程，直到包含元陣列的所有元素。整個合併過程可以參考下面取自 wiki 的圖：

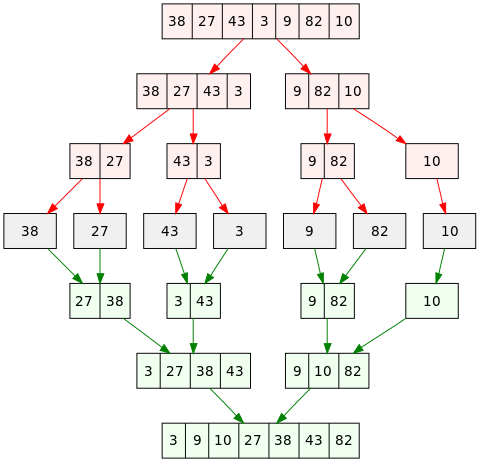
首先要先來研究一下如何合併兩個陣列。我們需要寫一個 mergeArray 方法，你可以直接使用 concat 之類的內建方法來合併兩個陣列，不過這裡我們練習一下 while 迴圈的操作，讓自己習慣一下：

function mergeArray(arrA, arrB) {
  const lengthA = arrA.length - 1;
  const lengthB = arrB.length - 1;
  const mergedArr = [];
  let indexA = 0;
  let indexB = 0;
  let indexMerged = 0;

  while (indexA <= lengthA && indexB <= lengthB) {
    // 先比較兩個陣列等長的部分，看誰的元素小，就先放入 mergedArray
    mergedArr[indexMerged++] = arrA[indexA] < arrB[indexB] ? arrA[indexA++] : arrB[indexB++];
  }

  // 可能是 arrB 先跑完，此時 arrA 還有剩
  while (indexA <= lengthA) {
    mergedArr[indexMerged++] = arrA[indexA++];
  }
  // 也可能是 arrA 先跑完，此時 arrB 還有剩
  while (indexB <= lengthB) {
    mergedArr[indexMerged++] = arrB[indexB++];
  }

  return mergedArr;
}

接著，我們需要一些輔助變數，因為合併時同時存在左陣列和右陣列。為了知道它們是否是鄰居關係，我們還需要還需要設置一個頂點，方便往上找上一層的陣列，這個上一層的陣列也要找它的鄰居進行合併。於是我們需要給陣列元素新增 top、left、right 屬性，用來分別引用切割後的子陣列和父陣列。

那麼在合併階段時，我們要怎麼知道當下是否處於合併階段呢，當陣列長度是 1 嗎？ 可是，如果再往上一層進行合併時，就不能繼續用這個條件了。因此我們需要多傳入一個參數 toMerge = true。像這樣分割後，就能一直進行合併。合併時，每個元素都要找到它的鄰居。首先要先知道自己是左邊還是右邊，然後再找到鄰居。對它的鄰居也要判斷是否已經排序過了。當一個陣列長度為 1，或者已經被調整過，我們就為它新增一個屬性 array.sorted = true。

function mergeSort(array, toMerge) {
  // 如果陣列還可以分割，並且處於分割模式
  if (array.length > 1 && toMerge !== true) {
    const top = array;
    const mid = ~~(array.length/2);
    top.left = array.slice(0, mid);
    top.right = array.slice(mid);
    top.left.top = top;
    top.right.top = top;
    console.log(top.left, top.right, '分割');
    mergeSort(top.left);
    mergeSort(top.right);
    // 如果陣列只剩下一個或是處於合併模式
  } else if (array.length === 1 || toMerge) {
    if (array.top && !array.merged) { // 如果左邊合併了右邊，那麼右邊就不用再合併左邊
      const isLeft = array === array.top.left;
      const neighbor = isLeft ? array.top.right : array.top.left;
      if (neighbor.length === 1 || neighbor.sorted) {
        const temp = mergeArray(array, neighbor);
        neighbor.merged = true; // 記錄已經合併過了
        console.log(temp, '合併');
        for (let i = 0; i < temp.length; i++) {
          array.top[i] = temp[i];
        }
        array.top.sorted = true;
        mergeSort(array.top, true);
      }
    }
  }
}

這次我們來換到瀏覽器上來看看，因為這個 log 會比較長：

在 main.js 匯入剛才的 mergeSort 然後貼上這段程式碼，執行 pnpm dev 打開 localhost:5173 然後打開控制台查看結果：

import { mergeSort } from '@/day20-merge-sort/MergeSort';

const arr = [3, 4, 9, 1, 8, 2, 0, 7, 6, 5];
mergeSort(arr);

/*
(5) [3, 4, 9, 1, 8, top: Array(10)] (5) [2, 0, 7, 6, 5, top: Array(10)] '分割'
(2) [3, 4, top: Array(5)] (3) [9, 1, 8, top: Array(5)] '分割'
[3, top: Array(2)] [4, top: Array(2)] '分割'
(2) [3, 4] '合併'
[9, top: Array(3)] (2) [1, 8, top: Array(3)] '分割'
[1, top: Array(2)] [8, top: Array(2)] '分割'
(2) [1, 8] '合併'
(3) [1, 8, 9] '合併'
(5) [1, 3, 4, 8, 9] '合併'
(2) [2, 0, top: Array(5)] (3) [7, 6, 5, top: Array(5)] '分割'
[2, top: Array(2)] [0, top: Array(2)] '分割'
(2) [0, 2] '合併'
[7, top: Array(3)] (2) [6, 5, top: Array(3)] '分割'
[6, top: Array(2)] [5, top: Array(2)] '分割'
(2) [5, 6] '合併'
(3) [5, 6, 7] '合併'
(5) [0, 2, 5, 6, 7] '合併'
(10) [0, 1, 2, 3, 4, 5, 6, 7, 8, 9] '合併'
*/

接著我們試著對其進行改進。因為我們使用了 slice 方法，創造了大量實質的陣列，佔用了大量的記憶體。事實上我們只需要一些虛擬的陣列即可，只要知道它們的第一個元素和最後一個元素在原始陣列的索引值，就能算出這些虛擬陣列。調整後的程式碼如下：

function mergeSortObject(array) {
  function sort(obj, toMerge) {
    // 如果陣列還可以分割，並且處於分割模式
    const { array, begin, end } = obj;
    const n = end - begin;
    if (n !== 0 && toMerge !== true) {
      const mid = begin + Math.floor(n / 2);
      obj.left = {
        begin: begin,
        end: mid,
        array: array,
        top: obj,
      };
      obj.right = {
        begin: mid + 1,
        end: end,
        array: array,
        top: obj,
      };
      sort(obj.left);
      sort(obj.right);
      // 如果陣列只剩下一個或是處於合併模式
    } else if (n === 0 || toMerge) {
      if (obj.top && !obj.merged) { // 如果左邊合併了右邊，那麼右邊就不用再合併左邊
        const top = obj.top;
        const isLeft = obj === top.left;
        const neighbor = isLeft ? top.right : top.left;
        if (neighbor.end == neighbor.begin || neighbor.sorted) {
          const temp = mergeArrayByIndex(array, begin, end, neighbor.begin, neighbor.end);
          neighbor.merged = true;
          const b = top.begin;
          for (let i = 0; i < temp.length; i++) {
            array[b + i] = temp[i];
          }
          top.sorted = true;
          sort(top, true);
        }
      }
    }
  }
  sort({
    array: array,
    begin: 0,
    end: array.length - 1,
  });
  return array;
}

mergeArray 方法也需要改成 mergeArrayByIndex：

function mergeArrayByIndex(arr, begin, end, begin2, end2) {
  let indexA = begin;
  let indexB = begin2;
  let indexMerged = 0;
  const mergedArr = [];

  while (indexA <= end && indexB <= end2) {
    // 先比較兩個陣列等長的部分，看誰的元素小，就先放入 mergedArray
    mergedArr[indexMerged++] = arr[indexA] < arr[indexB] ? arr[indexA++] : arr[indexB++];
  }

  while (indexA <= end) {
    mergedArr[indexMerged++] = arr[indexA++];
  }

  while (indexB <= end2) {
    mergedArr[indexMerged++] = arr[indexB++];
  }

  return mergedArr;
}

再仔細想想，其實我們也不需要 top 這個屬性，因為 top 屬性的存在是為了方變我們找 neighbor 元素的。如果我們在經過兩次 mergeSort 操作後，立即進行合併操作，就不需要 neighbor 了。接著將程式碼修改成這樣：

function mergeSortObject2(array) {
  function sort(obj, toMerge) {
    // 如果陣列還可以分割，並且處於分割模式
    const { array, begin, end } = obj;
    const n = end - begin;
    if (n !== 0 && toMerge !== true) {
      const mid = begin + Math.floor(n / 2);
      obj.left = {
        begin: begin,
        end: mid,
        array: array,
      };
      obj.right = {
        begin: mid + 1,
        end: end,
        array: array,
      };
      sort(obj.left);
      sort(obj.right);
      const temp = mergeArrayByIndex(array, begin, mid, mid + 1, end);
      for (let i = 0; i < temp.length; i++) {
        array[begin + i] = temp[i];
      }
    }
  }
  sort({
    array: array,
    begin: 0,
    end: array.length - 1,
  });
  return array;
}

這時我們又發現到，這個 sort 方法的第一個參數 obj 可以從物件改回陣列，第二個參數 toMerge 也可以刪除：

function mergeSortSimple(array) {
  function sort(array, begin, end) {
    // 如果陣列還可以分割，並且處於分割模式
    if (begin !== end) {
      const mid = begin + Math.floor((end - begin) / 2);
      sort(array, begin, mid);
      sort(array, mid + 1, end);
      const temp = mergeArrayByIndex(array, begin, mid, mid + 1, end);
      for (let i = 0; i < temp.length; i++) {
        array[begin + i] = temp[i];
      }
    }
  }
  sort(array, 0, array.length - 1);
  return array;
}

這就是一般在網路上常看到的版本，它就是這樣一步步最佳化而來的。我們把上面的程式碼拿來跑耗時測試：

========
部分有序的情況 bubbleSort3 7
完全亂序的情況 bubbleSort3 376
========
部分有序的情況 shellSort 5
完全亂序的情況 shellSort 3
========
部分有序的情況 mergeSort 10
完全亂序的情況 mergeSort 11
========
部分有序的情況 mergeSortObject 11
完全亂序的情況 mergeSortObject 5
========
部分有序的情況 mergeSortObject2 7
完全亂序的情況 mergeSortObject2 5
========
部分有序的情況 mergeSortSimple 3
完全亂序的情況 mergeSortSimple 2

最後，如果你不在意空間消耗的話，也可以簡單利用 JavaScript 內建的 slice 還有 concat 來實作：

function mergeSort2(array) {
  if (array.length > 1) {
    const n = array.length;
    const mid = Math.floor(n / 2);

    const left = mergeSort2(array.slice(0, mid));
    const right = mergeSort2(array.slice(mid, n));
    array = mergeSortedArrays(left, right);
  }
  return array;
}

function mergeSortedArrays(left, right) {
  const sortedArray = [];
  let leftIndex = 0;
  let rightIndex = 0;

  while (leftIndex < left.length && rightIndex < right.length) {
    sortedArray.push(
      left[leftIndex] <= right[rightIndex] ? left[leftIndex++] : right[rightIndex++]
    );
  }

  return sortedArray.concat(
    leftIndex < left.length ? left.slice(leftIndex) : right.slice(rightIndex)
  );
}

複雜度 Complexity

最後我們來看一下它的複雜度。其空間複雜度為 $O(n)$，因為它申請了一個等長的陣列，會消耗一定的空間。如果用最初的版本，新建了這麼多的陣列，其空間複雜度可能就是 $O(n^2)$ 了。它的時間複雜度可以這樣簡單推導一下，我們每次要取中位數，一共對 $O(\log n)$ 層進行了切割合併的操作。每一層的合併操作都是 $O(n)$，所以這個演算法的時間複雜度為 $O(n\log n)$。

Name	Average	Best	Worst	Space	Method	Stable
Merge sort	$O(n\log n)$	$O(n\log n)$	$O(n\log n)$	$O(n)$	Out-place	Yes

參考資料

• 《JavaScript 算法：基本原理與代碼實現》
• 《Learning JavaScript Data Structures and Algorithms, 3/e》
• Wikipedia